Resumen del libro
El arte de la estrategia
Por: Avinash K. Dixit Barry J. Nalebuff
Teoría de juegos aplicada al éxito empresarial
Introducción
Suponga que las circunstancias de la vida le imponen un escabroso duelo con dos pistoleros mucho más diestros que usted; el primero, llamado Adán, tiene un 80% de precisión en sus disparos, mientras que el segundo, Zoe, es un tirador perfecto, nunca falla. Usted, en cambio, inexperto en armas, apenas tiene un 30% de probabilidades de acertar el tiro. Ahora suponga que los tres están ubicados en las esquinas de un triángulo y que cada uno tendrá dos oportunidades de disparar, en dos rondas diferentes, cada una de las cuales comienza en usted y termina en Zoe. El mejor resultado, por supuesto, es ser el único superviviente. Pues bien, usted comienza, ya tiene en sus manos el arma con una sola bala: ¿qué hace?
Aunque la probabilidad de encontrarse en la situación descrita es infinitamente pequeña, el tipo de razonamiento que se requiere en ella para salir adelante es el mismo que usted utiliza diariamente para enfrentarse a todas esas situaciones en las que tiene que tomar la mejor decisión individual, teniendo en cuenta que se enfrenta a otras personas y que ellas, a su vez, intentan adoptar la decisión más adecuada a sus propios intereses. Pensar estratégicamente es el arte de superar a los adversarios, a sabiendas de que ellos también intentan hacer lo mismo. Por eso, el pensamiento estratégico no es una cuestión limitada a los juegos o a la guerra, sino algo que todos ponemos en práctica en el trabajo, en casa y en todas las dimensiones de la vida social. Y aunque hacerlo bien en tantos y tan diversos contextos no deja de ser un arte, los fundamentos del pensamiento estratégico se pueden reducir a unos cuantos principios básicos, tal como lo viene demostrando desde hace algunas décadas la joven ciencia de la teoría de juegos.
Volvamos por un instante a su duelo con Adán y Zoe. Si usted dispara a Adán y tiene el tino para acertar, entonces el arma pasará a Zoe, quien necesariamente le disparará a usted con una probabilidad del 100% de matarlo. Ahora bien, si usted le dispara a Zoe y lo mata, entonces va a ser Adán quien le dispare a usted, y su probabilidad de morir será del 80%. ¿Qué es lo mejor que puede hacer? ¡Disparar al aire! Dejar que sean ellos quienes se ataquen entre sí. Cuando el arma pase a Adán, él intentará matar a Zoe. Si lo mata, ahora usted disparará contra Adán (con un 30% de oportunidad de acierto) y, de no matarlo, tendrá un 20% de probabilidades de que él falle su último tiro. Si, por el contrario, Adán no acierta a matar a Zoe, Zoe acabará con él, pues representa una amenaza mayor, y a usted le quedará una última oportunidad de dispararle a Zoe y salvar su vida. En este, como en muchos otros escenarios, la mejor decisión en la primera jugada consiste en no hacer nada. Muchos políticos, por ejemplo, saben que es mejor entrar en escena cuando los rivales más fuertes ya se han hecho daño entre ellos.
La teoría de juegos analiza ese tipo de situaciones en que los individuos toman decisiones estando rodeados de otras personas que, a su vez, también toman decisiones. Y como sucede en el mercado de valores, en una partida de ajedrez, en una campaña política o en una relación de pareja, lo que haga cada una de las partes tendrá una incidencia directa sobre lo que harán las otras. Es ingenuo pretender trazar una fórmula abstracta para tomar siempre las mejores decisiones estratégicas, pues cada situación concreta tiene múltiples particularidades, pero los patrones de la interrelación obedecen a ciertas reglas observables, y esto permite esbozar algunos principios generales para orientar cualquier decisión estratégica. Más que fórmulas de éxito, estos principios son herramientas útiles para guiar su análisis de cada situación e intentar el desarrollo de la estrategia que más convenga a sus propios intereses.
Juegos de turno consecutivo
La teoría de juegos denomina juego a cualquier situación de interdependencia estratégica, es decir, todo escenario en el que el resultado de las decisiones o estrategias de un jugador dependa de lo que elija el otro o los otros jugadores, quienes también actúan con un propósito. Ahora bien, en algunos juegos, los intereses de los jugadores pueden estar en estricto conflicto y lo que una persona gana es siempre lo que la otra pierde. El póquer es un claro ejemplo de los denominados juegos de suma cero: si en este tipo de juegos uno suma las ganancias totales de los jugadores y les resta las pérdidas totales, el resultado será cero. Pero, por lo general, las situaciones son un poco más complejas y, junto con los intereses en conflicto, se conjugan algunos intereses comunes, dando lugar a combinaciones de estrategias que pueden ser mutuamente beneficiosas o mutuamente perjudiciales. Cuando dos empresas compiten por el mercado de la telefonía, el monto de sus ganancias podrá variar en función de las estrategias que cada una de ellas implemente. Así, si se declaran una guerra de precios y cada una intenta cobrar menos que la otra, su margen de beneficio tenderá a ser cada vez menor; pero si, por el contrario, actúan de forma coordinada para repartirse y explotar el mercado, las utilidades de cada una pueden aumentar de forma exponencial.
La esencia de un juego de estrategia, entonces, radica en la interdependencia existente entre las decisiones de los jugadores. Esa interacción se puede dar de dos formas: consecutiva o simultánea. En los juegos de turnos consecutivos, cada jugador juega en su turno y, por lo tanto, se puede utilizar un razonamiento lineal para predecir los efectos de una jugada: “si yo hago esto, mi adversario puede hacer aquello, con lo que yo a mi vez puedo responder de otra manera”. Estos juegos se pueden estudiar dibujando un árbol de juego, es decir, un diagrama en el que se trazan todas las jugadas posibles y para cada una de ellas se determinan las ramificaciones o posibles respuestas del contrincante, repitiendo el ejercicio en forma secuencial para luego evaluar cuál es el mejor camino a seguir. El tipo de razonamiento de un jugador de ajedrez es una muestra clara, aunque incompleta, de lo que significa trazar un árbol de estrategias: “si muevo ese peón, mi contrincante adelantará su caballo, amenazando mi torre. Si, mejor, muevo el alfil, protejo la torre, pero mi contrincante podrá mover su reina o adelantar su peón…”. Lo que sucede en la mente del jugador es apenas un bosquejo de un complejísimo árbol de juego, demasiado complejo como para que incluso una máquina pueda trazarlo con precisión, porque, si a cada una de las 20 jugadas posibles que tiene quien abre la partida le corresponden las 20 jugadas posibles de su contrincante, de cada una de estas 400 ramas se desprende un número mayor de alternativas, que siguen creciendo de forma exponencial, de manera que para prever todas las eventuales respuestas de un rival dentro de tres jugadas, habría que trazar un árbol con mas de cien millones de ramas. Por eso, más allá de ciertas estrategias para garantizar el triunfo o las tablas en una partida en la que el tablero ha quedado reducido a tres o cuatro piezas, las ramificaciones en el ajedrez son tantas, que los jugadores se ven abocados a combinar el análisis con sus juicios de valor.
Pero los árboles de juego no siempre son así de complejos y, en muchas ocasiones, permiten trazar un mapa completo de las posibles consecuencias de una acción. Suponga que Rapilimpia está evaluando la posibilidad de entrar a competir en el mercado de aspiradoras de Jamaica, que actualmente está monopolizado por Neolimpia. En tal caso, puede anticipar las eventuales consecuencias de su decisión trazando un árbol en el que identifica, y de paso cuantifica, todos los escenarios posibles. Así, sus alternativas iniciales son entrar a competir o no hacerlo. En el segundo caso no pasa nada y Neolimpia sigue con su monopolio; pero en el primero se abren dos alternativas: (1) que Neolimpia se acomode a la competencia y acepte reducir su cuota de mercado o (2) que Neolimpia decida entablar una guerra de precios. Suponga que, en su monopolio, Neolimpia obtiene beneficios de hasta 3 millones de euros, pero que si tuviera que compartir el mercado, esos beneficios se reducirían a un millón para cada una y que, en caso de entablar una guerra de precios, ya no tendrá ganancias, sino pérdidas. Al razonar así, Rapilimpia puede ver que sí le conviene entrar al mercado, pues la jugada óptima de Neolimpia será compartir el mercado y reducir sus ganancias, en lugar de enfrascarse en una guerra que le reportará cuantiosas pérdidas. Este sería, gráficamente, el árbol de decisiones:
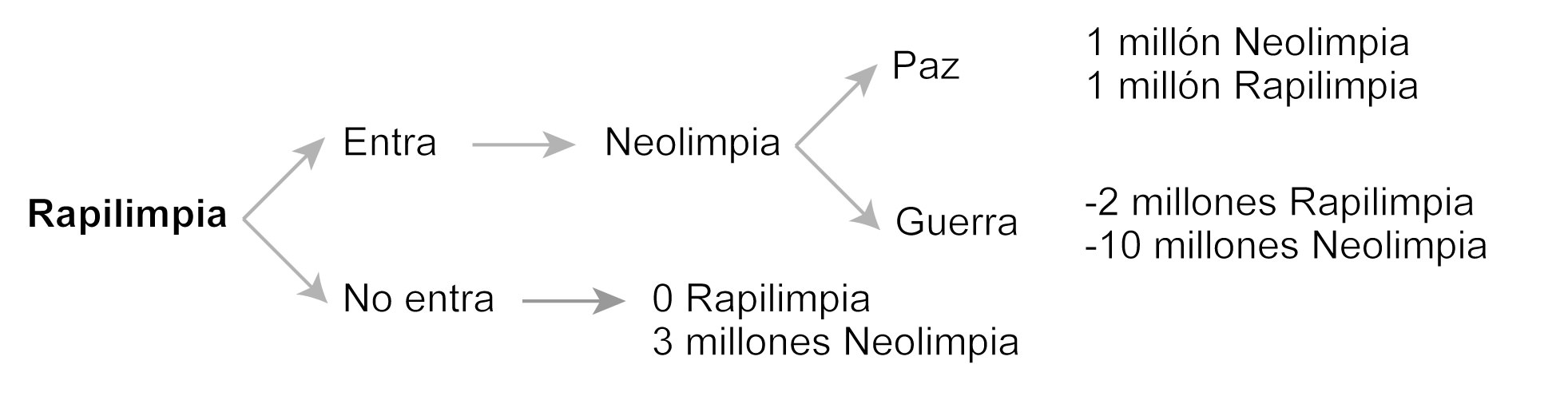
En la vida real, las circunstancias suelen tener más detalles que complican las cosas. Si, por ejemplo, existe la posibilidad de que Rapilimpia se introduzca después en otras islas del Caribe en las que Neolimpia tiene establecido su mercado, entonces esta última tendrá un incentivo diferente para establecer la guerra de precios y mostrarse como una contendora inquebrantable, asumiendo las pérdidas que esto le reporte. Si las cosas son así, Rapilimpia podrá prever de antemano las consecuencias de su acción, al saber que su ingreso en la primera isla le supondrá una pérdida de 2 millones de euros, con lo que se abstendrá de introducirse en ese mercado.
La primera regla de la teoría de juegos es esa: mirar hacia adelante y razonar hacia atrás. Prever todas las posibles consecuencias de una acción y, al identificar el resultado más conveniente, observar cuál es el camino que conduce hacia él. Esta regla resulta de gran utilidad en muchas situaciones reales en las que los turnos de acción se suceden de forma consecutiva. Las negociaciones son un ejemplo de ello. Aunque las hay de diversos estilos, y en algunas de ellas el margen de acción de una de las partes es bastante limitado (como las del estilo “lo toma o lo deja”), en muchos casos la negociación se funda en la alternancia de las proposiciones: una parte ofrece, la otra hace una contraoferta, la primera replica y así sucesivamente. Pues bien, un rasgo central de las negociaciones es que en ellas el tiempo es oro: cuando la negociación empieza a prolongarse, la tarta se va encogiendo. En Bleak House, de Charles Dickens, la disputa sobre las propiedades de Jarndyce se prolongó durante tanto tiempo, que solo el coste de los abogados se tragó la propiedad entera. Algo semejante sucede con las negociaciones salariales entre una empresa y el sindicato: cada día de huelga implica una reducción significativa en los beneficios a repartir.
Para continuar leyendo
Biografía del autor
Avinash K. Dixit
Avinash K. Dixit, economista estadounidense de origen indio, es profesor emérito de Economía en la Universidad de Princeton. Su primer libro, Thinking strategically: The competitive edge in business, politics and everyday life, fue un texto popular en las escuelas de negocio que se tradujo a siete idiomas y fue número 1 de ventas en Japón.
Barry J. Nalebuff
Barry J. Nalebuff es profesor en la escuela de Administración de Yale, en New Haven, Connecticut, y ha sido consultor de American Express, Bell Atlantic, Citibank, Corning, Merck y Procter & Gamble, entre otros.
Descargar Resumen
Descargas bloqueadashelp_outline
Comprar el libro
Si has leído el resumen y quieres profundizar más, te recomendamos comprar el libro completo, en papel o ebook, haciendo click aquí
Luis Alejandro Agudelo
Mira hacia adelante, razona hacia atrás. Es un libro fundamental para todos los líderes que cuando toman una decisión estas afectan su negocio. Pensar estratégicamente es adelantarse a las jugadas de tus competidores aunque en ocasiones "la mejor opción para cada uno es lo que es mejorar para mi rival"